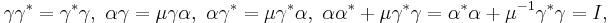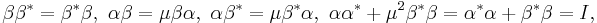Quantum group
| Group theory |
|---|
| Group theory |
|
Cyclic group Zn
Symmetric group, Sn Dihedral group, Dn Alternating group An Mathieu groups M11, M12, M22, M23, M24 Conway groups Co1, Co2, Co3 Janko groups J1, J2, J3, J4 Fischer groups F22, F23, F24 Baby Monster group B Monster group M |
|
|
|
Solenoid (mathematics)
Circle group General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) Lorentz group Poincaré group Conformal group Diffeomorphism group Loop group Infinite-dimensional Lie groups O(∞) SU(∞) Sp(∞) |
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra. There is no single, all-encompassing definition, but instead a family of broadly similar objects.
The term "quantum group" often denotes a kind of noncommutative algebra with additional structure that first appeared in the theory of quantum integrable systems, and which was then formalized by Vladimir Drinfel'd and Michio Jimbo as a particular class of Hopf algebra. The same term is also used for other Hopf algebras that deform or are close to classical Lie groups or Lie algebras, such as a `bicrossproduct' class of quantum groups introduced by Shahn Majid a little after the work of Drinfeld and Jimbo.
In Drinfeld's approach, quantum groups arise as Hopf algebras depending on an auxiliary parameter q or h, which become universal enveloping algebras of a certain Lie algebra, frequently semisimple or affine, when q = 1 or h = 0. Closely related are certain dual objects, also Hopf algebras and also called quantum groups, deforming the algebra of functions on the corresponding semisimple algebraic group or a compact Lie group.
Just as groups often appear as symmetries, quantum groups act on many other mathematical objects and it has become fashionable to introduce the adjective quantum in such cases; for example there are quantum planes and quantum Grassmannians.
Contents |
Intuitive meaning
The discovery of quantum groups was quite unexpected, since it was known for a long time that compact groups and semisimple Lie algebras are "rigid" objects, in other words, they cannot be "deformed". One of the ideas behind quantum groups is that if we consider a structure that is in a sense equivalent but larger, namely a group algebra or a universal enveloping algebra, then a group or enveloping algebra can be "deformed", although the deformation will no longer remain a group or enveloping algebra. More precisely, deformation can be accomplished within the category of Hopf algebras that are not required to be either commutative or cocommutative. One can think of the deformed object as an algebra of functions on a "noncommutative space", in the spirit of the noncommutative geometry of Alain Connes. This intuition, however, came after particular classes of quantum groups had already proved their usefulness in the study of the quantum Yang-Baxter equation and quantum inverse scattering method developed by the Leningrad School (Ludwig Faddeev, Leon Takhtajan, Evgenii Sklyanin, Nicolai Reshetikhin and Korepin) and related work by the Japanese School.[1] The intuition behind the second, bicrossproduct, class of quantum groups was different and came from the search for self-dual objects as an approach to quantum gravity.[2]
Drinfel'd-Jimbo type quantum groups
One type of objects commonly called a "quantum group" appeared in the work of Vladimir Drinfel'd and Michio Jimbo as a deformation of the universal enveloping algebra of a semisimple Lie algebra or, more generally, a Kac-Moody algebra, in the category of Hopf algebras. The resulting algebra has additional structure, making it into a quasitriangular Hopf algebra.
Let 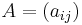 be the Cartan matrix of the Kac-Moody algebra, and let q be a nonzero complex number distinct from 1, then the quantum group,
be the Cartan matrix of the Kac-Moody algebra, and let q be a nonzero complex number distinct from 1, then the quantum group, 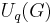 , where G is the Lie algebra whose Cartan matrix is A, is defined as the unital associative algebra with generators
, where G is the Lie algebra whose Cartan matrix is A, is defined as the unital associative algebra with generators 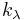 (where
(where  is an element of the weight lattice, i.e.
is an element of the weight lattice, i.e. 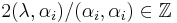 for all i), and
for all i), and 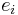 and
and 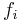 (for simple roots,
(for simple roots, 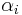 ), subject to the following relations:
), subject to the following relations:
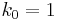 ,
,
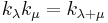 ,
,
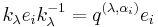 ,
,
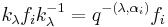 ,
,
![[e_i,f_j] = \delta_{ij} \frac{k_i - k_i^{-1}}{q_i - q_i^{-1}}](/2012-wikipedia_en_all_nopic_01_2012/I/8079694c8f2250e51b5e9e863cc71d9a.png) ,
,
![\sum_{n=0}^{1 - a_{ij}} (-1)^n \frac{[1 - a_{ij}]_{q_i}!}{[1 - a_{ij} - n]_{q_i}! [n]_{q_i}!} e_i^n e_j e_i^{1 - a_{ij} - n} = 0](/2012-wikipedia_en_all_nopic_01_2012/I/34ebac2d9e319987d66ac96824a7ee69.png) , for
, for 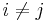 ,
,
![\sum_{n=0}^{1 - a_{ij}} (-1)^n \frac{[1 - a_{ij}]_{q_i}!}{[1 - a_{ij} - n]_{q_i}! [n]_{q_i}!} f_i^n f_j f_i^{1 - a_{ij} - n} = 0](/2012-wikipedia_en_all_nopic_01_2012/I/3d6c8345c5de372f0d48808e396b0df4.png) , for
, for 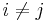 ,
,
where 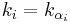 ,
, 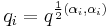 ,
, ![[0]_{q_i}! = 1](/2012-wikipedia_en_all_nopic_01_2012/I/880cca051f4b9d70760086ddbe1a1404.png) ,
, ![[n]_{q_i}! = \prod_{m=1}^n [m]_{q_i}](/2012-wikipedia_en_all_nopic_01_2012/I/d5074eb2faaa3468fb62c93b65d1d3c6.png) for all positive integers
for all positive integers  , and
, and ![[m]_{q_i} = \frac{q_i^m - q_i^{-m}}{q_i - q_i^{-1}}.](/2012-wikipedia_en_all_nopic_01_2012/I/f450e2f5cdad4c73e8fb7aa87c32eaa8.png) These are the q-factorial and q-number, respectively, the q-analogs of the ordinary factorial. The last two relations above are the q-Serre relations, the deformations of the Serre relations.
These are the q-factorial and q-number, respectively, the q-analogs of the ordinary factorial. The last two relations above are the q-Serre relations, the deformations of the Serre relations.
In the limit as 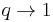 , these relations approach the relations for the universal enveloping algebra
, these relations approach the relations for the universal enveloping algebra 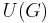 , where
, where 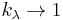 and
and 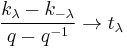 as
as 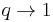 , where the element,
, where the element, 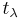 , of the Cartan subalgebra satisfies
, of the Cartan subalgebra satisfies 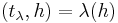 for all h in the Cartan subalgebra.
for all h in the Cartan subalgebra.
There are various coassociative coproducts under which these algebras are Hopf algebras, for example,
-
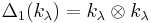 ,
, 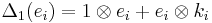 ,
, 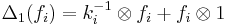 ,
,
-
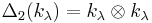 ,
, 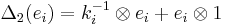 ,
, 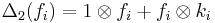 ,
,
-
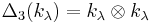 ,
, 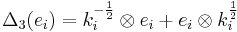 ,
, 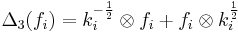 , where the set of generators has been extended, if required, to include
, where the set of generators has been extended, if required, to include 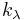 for λ which is expressible as the sum of an element of the weight lattice and half an element of the root lattice.
for λ which is expressible as the sum of an element of the weight lattice and half an element of the root lattice.
In addition, any Hopf algebra leads to another with reversed coproduct 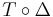 , where
, where  is given by
is given by 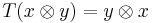 , giving three more possible versions.
, giving three more possible versions.
The counit on 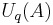 is the same for all these coproducts:
is the same for all these coproducts: 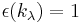 ,
, 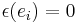 ,
, 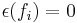 , and the respective antipodes for the above coproducts are given by
, and the respective antipodes for the above coproducts are given by
-
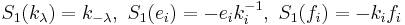 ,
,
-
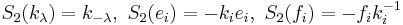 ,
,
Alternatively, the quantum group 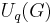 can be regarded as an algebra over the field
can be regarded as an algebra over the field 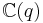 , the field of all rational functions of an indeterminate q over
, the field of all rational functions of an indeterminate q over 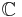 .
.
Similarly, the quantum group 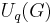 can be regarded as an algebra over the field
can be regarded as an algebra over the field 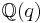 , the field of all rational functions of an indeterminate q over
, the field of all rational functions of an indeterminate q over 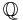 (see below in the section on quantum groups at q = 0). The center of quantum group can be described by quantum determinant.
(see below in the section on quantum groups at q = 0). The center of quantum group can be described by quantum determinant.
Representation theory
Just as there are many different types of representations for Kac-Moody algebras and their universal enveloping algebras, so there are many different types of representation for quantum groups.
As is the case for all Hopf algebras, 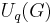 has an adjoint representation on itself as a module, with the action being given by
has an adjoint representation on itself as a module, with the action being given by 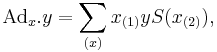 where
where 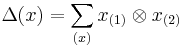 .
.
Case 1: q is not a root of unity
One important type of representation is a weight representation, and the corresponding module is called a weight module. A weight module is a module with a basis of weight vectors. A weight vector is a nonzero vector v such that 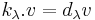 for all
for all  , where
, where 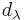 are complex numbers for all weights
are complex numbers for all weights  such that
such that
-
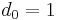 ,
,
-
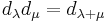 , for all weights
, for all weights  and
and  .
.
A weight module is called integrable if the actions of 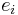 and
and 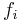 are locally nilpotent (i.e. for any vector v in the module, there exists a positive integer k, possibly dependent on v, such that
are locally nilpotent (i.e. for any vector v in the module, there exists a positive integer k, possibly dependent on v, such that 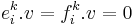 for all i). In the case of integrable modules, the complex numbers
for all i). In the case of integrable modules, the complex numbers 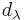 associated with a weight vector satisfy
associated with a weight vector satisfy 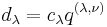 , where
, where  is an element of the weight lattice, and
is an element of the weight lattice, and 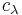 are complex numbers such that
are complex numbers such that
-
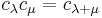 , for all weights
, for all weights  and
and  ,
,
-
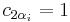 for all i.
for all i.
Of special interest are highest weight representations, and the corresponding highest weight modules. A highest weight module is a module generated by a weight vector v, subject to 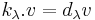 for all weights
for all weights  , and
, and 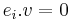 for all i. Similarly, a quantum group can have a lowest weight representation and lowest weight module, i.e. a module generated by a weight vector v, subject to
for all i. Similarly, a quantum group can have a lowest weight representation and lowest weight module, i.e. a module generated by a weight vector v, subject to 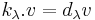 for all weights
for all weights  , and
, and 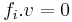 for all i.
for all i.
Define a vector v to have weight  if
if 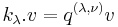 for all
for all  in the weight lattice.
in the weight lattice.
If G is a Kac-Moody algebra, then in any irreducible highest weight representation of 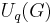 , with highest weight
, with highest weight  , the multiplicities of the weights are equal to their multiplicities in an irreducible representation of
, the multiplicities of the weights are equal to their multiplicities in an irreducible representation of 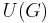 with equal highest weight. If the highest weight is dominant and integral (a weight
with equal highest weight. If the highest weight is dominant and integral (a weight  is dominant and integral if
is dominant and integral if  satisfies the condition that
satisfies the condition that 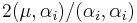 is a non-negative integer for all i), then the weight spectrum of the irreducible representation is invariant under the Weyl group for G, and the representation is integrable.
is a non-negative integer for all i), then the weight spectrum of the irreducible representation is invariant under the Weyl group for G, and the representation is integrable.
Conversely, if a highest weight module is integrable, then its highest weight vector v satisfies 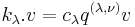 , where
, where 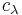 are complex numbers such that
are complex numbers such that
-
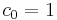 ,
,
-
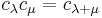 , for all weights
, for all weights  and
and  ,
,
-
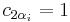 for all i,
for all i,
and  is dominant and integral.
is dominant and integral.
As is the case for all Hopf algebras, the tensor product of two modules is another module. For an element x of 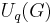 , and for vectors v and w in the respective modules,
, and for vectors v and w in the respective modules, 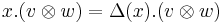 , so that
, so that 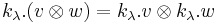 , and in the case of coproduct
, and in the case of coproduct 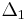 ,
, 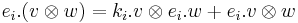 and
and 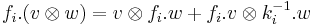 .
.
The integrable highest weight module described above is a tensor product of a one-dimensional module (on which 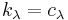 for all
for all  , and
, and 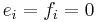 for all i) and a highest weight module generated by a nonzero vector
for all i) and a highest weight module generated by a nonzero vector 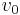 , subject to
, subject to 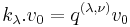 for all weights
for all weights  , and
, and 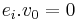 for all i.
for all i.
In the specific case where G is a finite-dimensional Lie algebra (as a special case of a Kac-Moody algebra), then the irreducible representations with dominant integral highest weights are also finite-dimensional.
In the case of a tensor product of highest weight modules, its decomposition into submodules is the same as for the tensor product of the corresponding modules of the Kac-Moody algebra (the highest weights are the same, as are their multiplicities).
Case 2: q is a root of unity
Quasitriangularity
Case 1: q is not a root of unity
Strictly, the quantum group 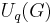 is not quasitriangular, but it can be thought of as being "nearly quasitriangular" in that there exists an infinite formal sum which plays the role of an R-matrix. This infinite formal sum is expressible in terms of generators
is not quasitriangular, but it can be thought of as being "nearly quasitriangular" in that there exists an infinite formal sum which plays the role of an R-matrix. This infinite formal sum is expressible in terms of generators 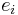 and
and 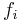 , and Cartan generators
, and Cartan generators 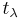 , where
, where 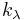 is formally identified with
is formally identified with 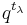 . The infinite formal sum is the product of two factors,
. The infinite formal sum is the product of two factors, 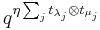 , and an infinite formal sum, where
, and an infinite formal sum, where 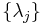 is a basis for the dual space to the Cartan subalgebra, and
is a basis for the dual space to the Cartan subalgebra, and 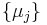 is the dual basis, and
is the dual basis, and 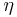 is a sign (+1 or -1).
is a sign (+1 or -1).
The formal infinite sum which plays the part of the R-matrix has a well-defined action on the tensor product of two irreducible highest weight modules, and also on the tensor product if two lowest weight modules. Specifically, if v has weight  and w has weight
and w has weight  , then
, then 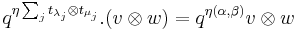 , and the fact that the modules are both highest weight modules or both lowest weight modules reduces the action of the other factor on
, and the fact that the modules are both highest weight modules or both lowest weight modules reduces the action of the other factor on  to a finite sum.
to a finite sum.
Specifically, if V is a highest weight module, then the formal infinite sum, R, has a well-defined, and invertible, action on  , and this value of R (as an element of
, and this value of R (as an element of 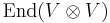 ) satisfies the Yang-Baxter equation, and therefore allows us to determine a representation of the braid group, and to define quasi-invariants for knots, links and braids.
) satisfies the Yang-Baxter equation, and therefore allows us to determine a representation of the braid group, and to define quasi-invariants for knots, links and braids.
Case 2: q is a root of unity
Quantum groups at q = 0
Masaki Kashiwara has researched the limiting behaviour of quantum groups as 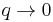 , and found a particularly well behaved base called a crystal base.
, and found a particularly well behaved base called a crystal base.
Description and classification by root-systems and Dynkin diagrams
There has been considerable progress in describing finite quotients of quantum groups such as the above 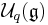 for
for 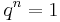 ; one usually considers the class of pointed Hopf algebras, meaning that all subcoideals are 1-dimensional and thus there sum form a group called coradical:
; one usually considers the class of pointed Hopf algebras, meaning that all subcoideals are 1-dimensional and thus there sum form a group called coradical:
- In 2002 H.-J. Schneider and N. Andruskiewitsch [3] finished their long-term classification effort of pointed Hopf algebras with coradical an abelian group (excluding primes 2, 3, 5, 7), especially as the above finite quotients of
 Just like ordinary Semisimple Lie algebra they decompose into E´s (Borel part), dual F´s and K´s (Cartan algebra):
Just like ordinary Semisimple Lie algebra they decompose into E´s (Borel part), dual F´s and K´s (Cartan algebra):
-
- Here, as in the classical theory V is a braided vector space of dimension n spanned by the E´s, and
 (a so-called cocylce twist) creates the nontrivial linking between E´s and F´s. Note that in contrast to classical theory, more than two linked components may appear. The role of the quantum Borel algebra is taken by a Nichols algebra
(a so-called cocylce twist) creates the nontrivial linking between E´s and F´s. Note that in contrast to classical theory, more than two linked components may appear. The role of the quantum Borel algebra is taken by a Nichols algebra 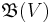 of the braided vectorspace.
of the braided vectorspace.
- Here, as in the classical theory V is a braided vector space of dimension n spanned by the E´s, and
- A crucial ingredience was hence the classification of finite Nichols algebras for abelian groups by I. Heckenberger [4] in terms of generalized Dynkin diagrams. When small primes are present, some exotic examples, such as a triangle, occur (see also the Figure of a rank 3 Dankin diagram).
- In the meanwhile, Schneider and Heckenbergen[5] have generally proven the existance of an arithmetic root system also in then nonabelian case, generating a PBW basis as proven by Kharcheko in the abelian case (without the assumption on finite dimension).
This could recently be used[6] on the specific cases 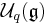 and explains e.g. the numerical coincidence between certain coideal subalgebras of these quantum groups to the order of the Weyl group of the Lie algebra
and explains e.g. the numerical coincidence between certain coideal subalgebras of these quantum groups to the order of the Weyl group of the Lie algebra  .
.
Compact matrix quantum groups
See also compact quantum group.
S.L. Woronowicz introduced compact matrix quantum groups. Compact matrix quantum groups are abstract structures on which the "continuous functions" on the structure are given by elements of a C*-algebra. The geometry of a compact matrix quantum group is a special case of a noncommutative geometry.
The continuous complex-valued functions on a compact Hausdorff topological space form a commutative C*-algebra. By the Gelfand theorem, a commutative C*-algebra is isomorphic to the C*-algebra of continuous complex-valued functions on a compact Hausdorff topological space, and the topological space is uniquely determined by the C*-algebra up to homeomorphism.
For a compact topological group, G, there exists a C*-algebra homomorphism 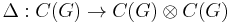 (where
(where  is the C*-algebra tensor product - the completion of the algebraic tensor product of
is the C*-algebra tensor product - the completion of the algebraic tensor product of 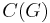 and
and 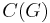 ), such that
), such that 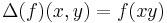 for all
for all 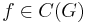 , and for all
, and for all 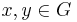 (where
(where 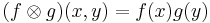 for all
for all 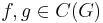 and all
and all 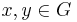 ). There also exists a linear multiplicative mapping
). There also exists a linear multiplicative mapping 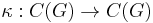 , such that
, such that 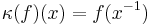 for all
for all 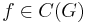 and all
and all 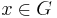 . Strictly, this does not make
. Strictly, this does not make 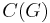 a Hopf algebra, unless G is finite. On the other hand, a finite-dimensional representation of G can be used to generate a *-subalgebra of
a Hopf algebra, unless G is finite. On the other hand, a finite-dimensional representation of G can be used to generate a *-subalgebra of 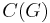 which is also a Hopf *-algebra. Specifically, if
which is also a Hopf *-algebra. Specifically, if 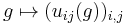 is an
is an  -dimensional representation of
-dimensional representation of  , then
, then 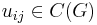 for all
for all 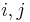 , and
, and 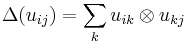 for all
for all 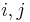 . It follows that the *-algebra generated by
. It follows that the *-algebra generated by 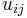 for all
for all 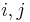 and
and 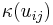 for all
for all 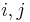 is a Hopf *-algebra: the counit is determined by
is a Hopf *-algebra: the counit is determined by 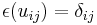 for all
for all 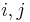 (where
(where 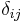 is the Kronecker delta), the antipode is
is the Kronecker delta), the antipode is  , and the unit is given by
, and the unit is given by 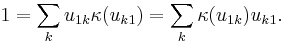
As a generalization, a compact matrix quantum group is defined as a pair 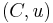 , where
, where  is a C*-algebra and
is a C*-algebra and 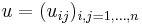 is a matrix with entries in
is a matrix with entries in  such that
such that
-
- The *-subalgebra,
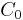 , of
, of  , which is generated by the matrix elements of
, which is generated by the matrix elements of  , is dense in
, is dense in  ;
;
- The *-subalgebra,
-
- There exists a C*-algebra homomorphism
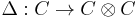 (where
(where  is the C*-algebra tensor product - the completion of the algebraic tensor product of
is the C*-algebra tensor product - the completion of the algebraic tensor product of  and
and  ) such that
) such that 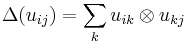 for all
for all 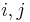 (
( is called the comultiplication);
is called the comultiplication);
- There exists a C*-algebra homomorphism
-
- There exists a linear antimultiplicative map
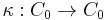 (the coinverse) such that
(the coinverse) such that 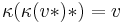 for all
for all 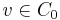 and
and 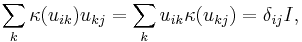 where
where  is the identity element of
is the identity element of  . Since
. Since  is antimultiplicative, then
is antimultiplicative, then 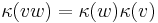 for all
for all 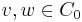 .
.
- There exists a linear antimultiplicative map
As a consequence of continuity, the comultiplication on  is coassociative.
is coassociative.
In general,  is not a bialgebra, and
is not a bialgebra, and 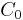 is a Hopf *-algebra.
is a Hopf *-algebra.
Informally,  can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and
can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and  can be regarded as a finite-dimensional representation of the compact matrix quantum group.
can be regarded as a finite-dimensional representation of the compact matrix quantum group.
A representation of the compact matrix quantum group is given by a corepresentation of the Hopf *-algebra (a corepresentation of a counital coassociative coalgebra  is a square matrix
is a square matrix 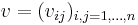 with entries in
with entries in  (so
(so 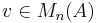 ) such that
) such that 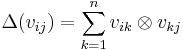 for all
for all 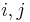 and
and 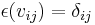 for all
for all 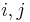 ). Furthermore, a representation v, is called unitary if the matrix for v is unitary (or equivalently, if
). Furthermore, a representation v, is called unitary if the matrix for v is unitary (or equivalently, if 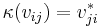 for all i, j).
for all i, j).
An example of a compact matrix quantum group is 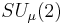 , where the parameter
, where the parameter  is a positive real number. So
is a positive real number. So 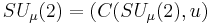 , where
, where 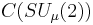 is the C*-algebra generated by
is the C*-algebra generated by  and
and  ,subject to
,subject to
and 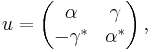 so that the comultiplication is determined by
so that the comultiplication is determined by 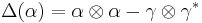 ,
, 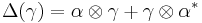 , and the coinverse is determined by
, and the coinverse is determined by 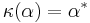 ,
, 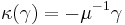 ,
,  ,
, 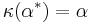 . Note that
. Note that  is a representation, but not a unitary representation.
is a representation, but not a unitary representation.  is equivalent to the unitary representation
is equivalent to the unitary representation 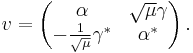
Equivalently, 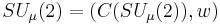 , where
, where 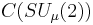 is the C*-algebra generated by
is the C*-algebra generated by  and
and  ,subject to
,subject to
and 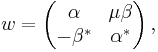 so that the comultiplication is determined by
so that the comultiplication is determined by 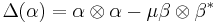 ,
, 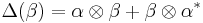 , and the coinverse is determined by
, and the coinverse is determined by 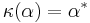 ,
, 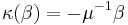 ,
,  ,
, 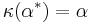 . Note that
. Note that  is a unitary representation. The realizations can be identified by equating
is a unitary representation. The realizations can be identified by equating 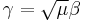 .
.
When 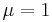 , then
, then 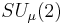 is equal to the algebra
is equal to the algebra 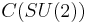 of functions on the concrete compact group
of functions on the concrete compact group 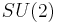 .
.
Bicrossproduct quantum groups
Whereas compact matrix pseudogroups are typically versions of Drinfeld-Jimbo quantum groups in a dual function algebra formulation, with additional structure, the bicrossproduct ones are a distinct second family of quantum groups of increasing importance as deformations of solvable rather than semisimple Lie groups. They are associated to Lie splittings of Lie algebras or local factorisations of Lie groups and can be viewed as the cross product or Mackey quantisation of one of the factors acting on the other for the algebra and a similar story for the coproduct  with the second factor acting back on the first. The very simplest nontrivial example corresponds to two copies of
with the second factor acting back on the first. The very simplest nontrivial example corresponds to two copies of 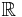 locally acting on each other and results in a quantum group (given here in an algebraic form) with generators
locally acting on each other and results in a quantum group (given here in an algebraic form) with generators 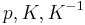 , say, and coproduct
, say, and coproduct
![[p,K]=h K(K-1)](/2012-wikipedia_en_all_nopic_01_2012/I/24cbfb4c9fa933275da837156cb3b8e5.png) ,
, 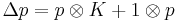 ,
, 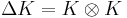
where  is the deformation parameter. This quantum group was linked to a toy model of Planck scale physics implementing Born reciprocity when viewed as a deformation of the Heisenberg algebra of quantum mechanics. Also, starting with any compact real form of a semisimple Lie algebra
is the deformation parameter. This quantum group was linked to a toy model of Planck scale physics implementing Born reciprocity when viewed as a deformation of the Heisenberg algebra of quantum mechanics. Also, starting with any compact real form of a semisimple Lie algebra  its complexification as a real Lie algebra of twice the dimension splits into
its complexification as a real Lie algebra of twice the dimension splits into  and a certain solvable Lie algebra (the Iwasawa decomposition), and this provides a canonical bicrossproduct quantum group associated to
and a certain solvable Lie algebra (the Iwasawa decomposition), and this provides a canonical bicrossproduct quantum group associated to  . For
. For 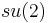 one obtains a quantum group deformation of the Euclidean group E(3) of motions in 3 dimensions.
one obtains a quantum group deformation of the Euclidean group E(3) of motions in 3 dimensions.
See also
Notes
- ^ Schwiebert, Christian (1994), Generalized quantum inverse scattering, pp. 12237, arXiv:hep-th/9412237v3, Bibcode 1994hep.th...12237S
- ^ Majid, Shahn (1988), "Hopf algebras for physics at the Planck scale", Classical and Quantum Gravity 5 (12): 1587–1607, Bibcode 1988CQGra...5.1587M, doi:10.1088/0264-9381/5/12/010
- ^ Andruskiewitsch, Schneider: Pointed Hopf algebras, New directions in Hopf algebras, 1–68, Math. Sci. Res. Inst. Publ., 43, Cambridge Univ. Press, Cambridge, 2002.
- ^ Heckenberger: Nichols algebras of diagonal type and arithmetic root systems, Habilitation thesis 2005.
- ^ Heckenberger, Schneider: Root system and Weyl gruppoid for Nichols algebras, 2008.
- ^ Heckenberger, Schneider: Right coideal subalgebras of Nichols algebras and the Duflo order of the Weyl grupoid, 2009.
References
- Podles, P.; Muller, E. (1997), Introduction to quantum groups, pp. 4002, arXiv:q-alg/9704002, Bibcode 1997q.alg.....4002P
- Kassel, Christian (1995), Quantum groups, Graduate Texts in Mathematics, 155, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94370-1, MR1321145
- Majid, Shahn (2002), A quantum groups primer, London Mathematical Society Lecture Note Series, 292, Cambridge University Press, ISBN 978-0-521-01041-2, MR1904789
- Street, Ross (2007), Quantum groups, Australian Mathematical Society Lecture Series, 19, Cambridge University Press, ISBN 978-0-521-69524-4; 978-0-521-69524-4, MR2294803.
- Majid, Shahn (January 2006), "What Is...a Quantum Group?" (PDF), Notices of the American Mathematical Society 53 (1): 30–31, http://www.ams.org/notices/200601/what-is.pdf, retrieved 2008-01-16
- Shnider, Steven; Sternberg, Shlomo (1993) Quantum groups. From coalgebras to Drinfel'd algebras. A guided tour. Graduate Texts in Mathematical Physics, II. International Press, Cambridge, MA.
- R. Jagannathan, Some introductory notes on quantum groups, quantum algebras, and their applications
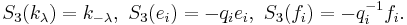
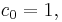
![\left(\mathfrak{B}(V)\otimes k[\mathbb{Z}^n]\otimes\mathfrak{B}(V^*)\right)^\sigma](/2012-wikipedia_en_all_nopic_01_2012/I/b3af675fbfc08b1df59a0874654c7287.png)